Сумма квадратов катетов в прямоугольном треугольнике равна квадрату гипотенузы. Это утверждение представляет собой знаменитую теорему Пифагора - одну из фундаментальных теорем евклидовой геометрии.
Содержание
Формулировка теоремы Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы (c) равен сумме квадратов длин катетов (a и b):
c2 = a2 + b2
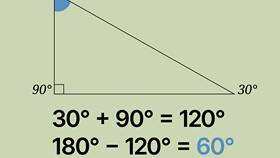
Геометрическая интерпретация
| Элемент | Описание |
| Катет a | Одна из двух сторон, образующих прямой угол |
| Катет b | Вторая сторона, образующая прямой угол |
| Гипотенуза c | Сторона, противолежащая прямому углу |
Примеры расчетов
Пример 1: Классический треугольник
Для треугольника с катетами 3 и 4:
- 32 + 42 = 9 + 16 = 25
- √25 = 5 (длина гипотенузы)
Пример 2: Равнобедренный треугольник
Для треугольника с равными катетами по 1:
- 12 + 12 = 1 + 1 = 2
- √2 ≈ 1.414 (длина гипотенузы)
Применение теоремы
- Вычисление расстояний между точками на плоскости
- Определение длин диагоналей прямоугольников
- Решение задач в строительстве и архитектуре
- Применение в физике для расчета векторов
Доказательства теоремы
Существует множество способов доказательства теоремы Пифагора:
- Через площади квадратов
- Алгебраические доказательства
- Геометрические преобразования
- Использование подобия треугольников
Историческая справка
Хотя теорема названа в честь древнегреческого математика Пифагора, она была известна задолго до него. Вавилонские клинописные таблички демонстрируют, что соотношение между сторонами прямоугольного треугольника было известно еще в древнем Вавилоне.
Обратная теорема
Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник прямоугольный. Это утверждение называется теоремой, обратной теореме Пифагора.
| Условие | Вывод |
| a2 + b2 = c2 | Треугольник прямоугольный |
| a2 + b2 > c2 | Треугольник остроугольный |
| a2 + b2< c2 | Треугольник тупоугольный |