Равнобедренный треугольник, как и любой другой треугольник, обладает определенными свойствами углов. Рассмотрим ключевые аспекты суммы углов в этой геометрической фигуре.
Содержание
Основное свойство суммы углов треугольника
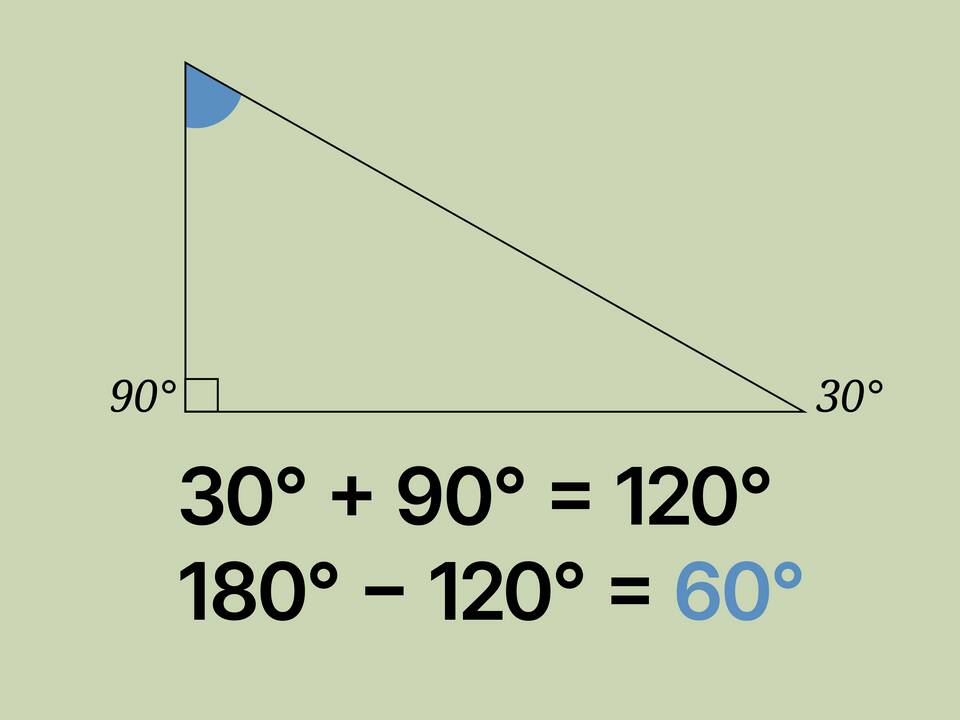
В любом треугольнике, независимо от его вида, сумма внутренних углов всегда равна 180 градусам. Это фундаментальное свойство евклидовой геометрии.
| Тип треугольника | Сумма углов |
| Равнобедренный | 180° |
| Равносторонний | 180° |
| Разносторонний | 180° |
Особенности равнобедренного треугольника
Определение равнобедренного треугольника
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона - основанием.
Свойства углов
- Углы при основании равны
- Биссектриса, медиана и высота, проведенные к основанию, совпадают
- Сумма всех трех углов составляет 180 градусов
Пример расчета углов
При известном угле при вершине
Если угол при вершине (между боковыми сторонами) равен 100°, то:
- Сумма углов при основании: 180° - 100° = 80°
- Каждый угол при основании: 80° / 2 = 40°
При известном угле при основании
| Угол при основании | Расчет остальных углов |
| 55° | Второй угол при основании: 55°, угол при вершине: 180° - (55° + 55°) = 70° |
| 60° | Все углы по 60° (частный случай - равносторонний треугольник) |
Доказательство суммы углов
Геометрическое доказательство
- Через вершину треугольника проводится прямая, параллельная основанию
- Образуются соответственные и накрест лежащие углы
- Сумма углов при прямой дает 180°
Практическое подтверждение
- Нарисовать равнобедренный треугольник
- Измерить транспортиром все углы
- Сложить полученные значения
- Результат всегда будет равен 180°
Вывод
Сумма углов равнобедренного треугольника, как и любого другого треугольника на плоскости, всегда равна 180 градусам. Это свойство не зависит от длин сторон или величины углов, являясь фундаментальным законом евклидовой геометрии.